Областью применения простых процентов чаще всего являются краткосрочные операции(со сроком до одного года) с однократным начислением процентов (краткосрочные ссуды, вексельные кредиты) и реже -- долгосрочные операции.

При краткосрочных операциях используется так называемая промежуточная процентная ставка, под которой понимается годовая процентная ставка, приведенная к сроку вложения денежных средств. Математически промежуточная процентная ставка равна доле годовой процентной ставки. Формула наращения простых процентов с использованием промежуточной процентной ставки имеет следующий вид:

FV = PV (1 + f * r),

FV = PV (1 + t * r / Т),

t -- срок вложения денежных средств (при этом день вложения и день изъятия денежных средств принимаются за один день); Т -- расчетное количество дней в году.

Придолгосрочныхоперациях начисление простых процентов рассчитывается по формуле:

FV = PV (1 + r * n),

где n -- срок вложения денежных средств (в годах). ,

Применение сложных процентов

Областью применения сложных процентов являются долгосрочные операции (со сроком, превышающим год), в том числе предполагающие внутригодовое начисление процентов.

В первом случае применяется обычная формула начисления сложных процентов:

FV = PV (1 + r)n.

Во втором случае применяется формула начисления сложных процентов с учетом внутригодового начисления. Под внутригодовым начислением процентов понимается выплата процентного дохода более одного раза в год. В зависимости от количества выплат дохода в год (m) внутригодовое начисление может быть:

1) полугодовым (m = 2);
2) поквартальным (m = 4);
3) ежемесячным (m = 12);
4) ежедневным (m = 365 или 366);
5) непрерывным (m -» ?).

Формула наращения при полугодовом, поквартальном, ежемесячном и ежедневном начислении сложных процентов имеет следующий вид:

FV = PV (1 + r / m)nm,

где PV -- исходная сумма;

г -- годовая процентная ставка;

n -- количество лет;

m -- количество внутригодовых начислений;

FV -- наращенная сумма.

Процентный доход при непрерывном начислении процентов рассчитывается по следующей формуле:

где: e = 2, 718281 -- трансцендентное число (число Эйлера);

е?n -- множитель наращения, который используется как при целом, так и дробном значении n;

Специальное обозначение процентной ставки при непрерывном начислении процентов (непрерывная процентная ставка, «сила роста»);

n -- количество лет.

При одинаковой величине исходной суммы, одинаковом сроке вложения денежных средств и значении процентной ставки возвращаемая сумма оказывается больше в случае использования формулы внутригодовых начислений, чем в случае использования обычной формулы начисления сложных процентов:

FV = PV (1 + r / m)nm> FV = PV (1 + r)n.

Если доход, полученный при использовании внутригодовых начислений, выразить в процентах, то полученная процентная ставка окажется выше той, которая использовалась при обычном начислении сложных процентов.

Таким образом, первоначально заявленная годовая процентная ставка для начисления сложных процентов, называемая номинальной, не отражает реальной эффективности сделки. Процентная ставка, отражающая фактически полученный доход, называется эффективной. Классификацию процентных ставок при внутригодовом начислении сложных процентов наглядно иллюстрирует рисунок.

Номинальная процентная ставка задается изначально. Для каждой номинальной процентной ставки и на ее основании можно рассчитать эффективную процентную ставку (rе).

Из формулы наращения сложных процентов можно получить формулу эффективной процентной ставки:

FV = PV (1 + r)n;

(1 + re) = FV / PV.

Приведем формулу наращения сложных процентов с внутригодовыми начислениями, при которых каждый год начисляется r / m процента:

FV = PV (1 + r / m)nm.

Тогда эффективная процентная ставка находится по формуле:

(1 + re) = (1 + r/m)m,

re = (l + r/m)m- 1,

где rе -- эффективная процентная ставка; r -- номинальная процентная ставка; m -- количество внутригодовых выплат.

Величина эффективной процентной ставки зависит от количества внутригодовых начислений (m):

1) при m = 1 номинальная и эффективная процентные ставки равны;
2) чем больше количество внутригодовых начислений (значение m), тем больше эффективная процентная ставка.

Областью одновременного применения простых и сложных процентов являются долгосрочные операции, срок которых составляет дробное количество лет. При этом начисление процентов возможно двумя способами:

1) начисление сложных процентов с дробным числом лет;
2) начисление процентов по смешанной схеме.

В первом случае для расчетов применяется формула сложных процентов, в которой присутствует возведение в дробную степень:

FV = PV (1 + r)n+f,

где f -- дробная часть срока вложения денежных средств.

Во втором случае для расчетов применяется так называемая смешанная схема, которая включает формулу начисления сложных процентов с целым числом лет и формулу начисления простых процентов для краткосрочных операций:

FV = PV (1 + r)n * (1 + f * r),

FV = PV (1 + r)n * (1 + t * r / Т) .

Общеизвестна ситуация, что одна и та же сумма денег неравноценна в разные периоды времени. Учет временного фактора в финансовых операциях осуществляется путем начисления процентов.

Процентными деньгами (процентами) называют сумму доходов от предоставления денег в долг в любой форме (выдача ссуд, открытие депозитных счетов, покупка облигаций, сдача оборудования в аренду и т.п.).

Сумма процентных денег зависит от суммы долга, срока его выплаты и процентной ставки, характеризующей интенсивность
начисления процентов. Сумму долга с начисленными процентами называют наращенной суммой. Отношение наращенной суммы к первоначальной сумме долга называют множителем (коэффициентом) наращения. Интервал времени, за который начисляются проценты, называют периодом начисления.

При использовании простых ставок процентов сумма процентных денег определяется исходя из первоначальной суммы долга, независимо от количества периодов начисления и их длительности по формуле:

Приведенная формула используется для определения величины наращенной стоимости капитала при краткосрочных финансовых вложениях.

Если срок долга задается в днях, в приведенную формулу надо вставить выражение:

где 5 - продолжительность периода начисления в днях;

Количество дней в году можно брать точно - 365 или 366 (точные проценты) или приближенно - 360 дней (обыкновенные проценты). Количество дней в каждом целом месяце в течение срока долга также может браться точно или приближенно (30 дней). В мировой банковской практике использование:

приближенного количества дней в каждом целом месяце и обыкновенных процентов называется «германской практикой»;

точного числа дней в каждом месяце и обыкновенных процентов - «французской практикой»;

точного числа дней и точных процентов - «английской практикой».

В зависимости от использования конкретной практики начисления процентов их сумма будет различаться.

Рассмотрим примеры финансово-экономических расчетов по ценным бумагам.

Пример 7.1.

Сберегательный сертификат номиналом 200 тыс. руб. выдан 20.01.2005г. с погашением 05.10.2005г. под 7,5% годовых.

Определить сумму начисленных процентов и цену погашения сертификата при использовании различных способов начисления процентов.

Определим точное и приближенное количество дней до погашения сертификата.

tT04H = 11 дней января + 28 дней февраля + 31 день марта + 30 дней апреля + 31 день мая + 30 дней июня + 31 день июля + 31 день августа + 30 дней сентября + 5 дней октября = 258 дней.

Іприбл = 11 дней января + 30 х 8 дней (февраль - сентябрь) + 5 дней октября = 256 дней.

По сертификатам доход начисляется по процентной ставке. Применим три способа расчета процентов:

1) проценты точные, срок займа - точное число дней:

Іточн = 0,075 х 200 х 258/365 = 10,6 тыс. руб.; цена погашения сертификата:

51 = 200 + 10,6 = 210,6 тыс. руб.;

2) проценты обыкновенные, срок займа - точное число дней, цена погашения сертификата:

52 = 200 + 10,8 = 210,8 тыс. руб.;

3) проценты обыкновенные, срок займа - приближенное число

Іобьікн = 0,075 х 200 х 256/360 = 10,7 тыс. руб., цена погашения сертификата:

53 = 200 + 10,7 = 210,7 тыс. руб.

Пример 7.2.

Банк принимает депозиты на 3 месяца по ставке 4% годовых, на 6 месяцев по ставке 10% годовых и на год по ставке 12% годовых. Определить сумму, которую получит владелец депозита 50 тыс. руб. во всех трех случаях.

Сумма депозита с процентами составит:

1) при сроке 3 месяца:

S = 50 х (1 + 0,25 х 0,04) = 50,5 тыс. руб.;

2) при сроке 6 месяцев:

S = 50 х (1 + 0,5 х 0,1) = 52,5 тыс. руб.;

3) при сроке 1 год:

S = 50 х (1 + 1 х 0,12) = 56 тыс. руб.

При принятии решения о размещении средств в банке немаловажным фактором является соотношение ставки процента и уровня инфляции. Уровень инфляции показывает, на сколько процентов выросли цены за рассматриваемый период времени, и определяется как:

Индекс инфляции показывает, во сколько раз выросли цены за рассматриваемый период. Уровень инфляции и индекс инфляции за один и тот же период связаны соотношением:

где Ju - индекс инфляции за период;

N - количество периодов в течение рассматриваемого срока.

Уровень инфляции за период.

Пример 7.3.

Определить ожидаемый годовой уровень инфляции при уровне инфляции за месяц в 6 и 12%.

Ju = (1 + 0,06)12 = 2,01.

Следовательно, ожидаемый годовой уровень инфляции будет равен = 2,01 - 1 = 1,01, или 101%.

Ju = (1 + 0,12)12 = 3,9.

Ожидаемый уровень инфляции будет равен:

3,9 - 1 = 2,9, или 290%.

Инфляция влияет на доходность финансовых операций.

Реальное значение наращенной суммы с процентами за предельный срок, приведенное к моменту предоставления денег в долг, составит:

Пример 7.4.

Банк принимает депозиты на полгода по ставке 9% годовых. Определить реальные результаты вкладной операции для вклада 1000 тыс. руб. при месячном уровне инфляции 8%.

Сумма вклада с процентами составит:

S = 1 х (1 + 0,5 х 0,09) = 1045 тыс. руб.

Индекс инфляции за срок хранения депозита равен:

Ju = (1 + 0,08)6 = 1,59.

Наращенная сумма с учетом инфляции будет соответствовать сумме:

1045/1,59 = 657 тыс. руб.

При использовании сложных ставок процентов процентные деньги, начисленные после первого периода начисления, являющегося частью общего срока долга, присоединяются к сумме долга. Во втором периоде начисления проценты будут начисляться исходя из первоначальной суммы долга, увеличенной на сумму процентов, начисленных после первого периода начисления, и так далее на каждом последующем периоде начисления. Если сложные проценты начисляются по постоянной ставке и все периоды начисления имеют одинаковую длительность, то наращенная сумма будет равна:

где P - первоначальная сумма долга;

in - ставка процентов в периоде начисления;

п - количество периодов начисления в течение срока.

Пример 7.5.

Депозит 50 тыс. руб. положен в банк на 3 года с начислением сложных процентов по ставке 8% годовых. Определить сумму начисленных процентов.

Сумма депозита с начисленными процентами будет равна:

S = 50 х (1 + 0,08)3 = 63 тыс. руб.

Сумма начисленных процентов составит:

I = S - Р = 63 - 50 = 13 тыс. руб.

Если бы проценты начислялись по простой ставке 8% годовых, сумма их составила бы:

I = 3 х 0,08 х 50 = 12 тыс. руб.

Таким образом, начисление процентов по сложной ставке дает большую сумму процентных денег.

Сложные проценты могут начисляться несколько раз в году. При этом годовую ставку процентов, исходя из которой определяется величина процентов в каждом периоде начисления, называют
номинальной годовой ставкой процентов. При сроке долга п лет и начислении сложных процентов m раз в году общее количество периодов начисления будет равно:

Наращенная сумма будет равна:

1) срок долга:

Пример 7.6.

Вкладчик вносит депозит 40 тыс. руб. на 2 года под номинальную ставку 40% годовых при ежемесячном начислении и капитализации процентов. Определить наращенную сумму и величину начисленных процентов.

Количество периодов начисления равно:

Следовательно, наращенная сумма составит:

Вексель или другое денежное обязательство до наступления срока платежа по нему могут быть куплены банком по цене, меньше суммы, которая должна быть выплачена по ним в конце срока, или, как принято говорить, учтены банком с дисконтом. Предъявитель обязательства при этом получает деньги ранее указанного в нем срока за вычетом дохода
банка в виде дисконта. Банк при наступлении срока оплаты векселя или иного обязательства получает полностью указанную в нем сумму.

Если срок от момента учета до момента погашения обязательства будет составлять некоторую часть года, дисконт будет равен.

6.2 Применение пределов в экономических расчетах

Сложные проценты

В практических расчетах в основном применяют дискретные проценты, т.е. проценты, начисляемые за фиксированные одинаковые интервалы времени (год, полугодие, квартал и т. д.). Время - дискретная переменная. В некоторых случаях - в доказательствах и расчетах, связанных с непрерывными процессами, возникает необходимость в применении непрерывных процентов. Рассмотрим формулу сложных процентов:

S = P(1 + i) n . (6.16)

Здесь P - первоначальная сумма, i - ставка процентов (в виде десятичной дроби), S - сумма, образовавшаяся к концу срока ссуды в конце n-го года. Рост по сложным процентам представляет собой процесс, развивающийся по геометрической прогрессии. Присоединение начисленных процентов к сумме, которая служила базой для их определения, часто называют капитализацией процентов. В финансовой практике часто сталкиваются с задачей, обратной определению наращенной суммы: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды P. В этом случае говорят, что сумма S дисконтируется, а проценты в виде разности S - P называются дисконтом. Величину P, найденную дисконтированием S, называют современной, или приведенной, величиной S. Имеем:

P = Þ P = = 0.

Таким образом, при очень больших сроках платежа современная величина последнего будет крайне незначительна.

В практических финансово-кредитных операциях непрерывные процессы наращения денежных сумм, т. е. наращения за бесконечно малые промежутки времени, применяются редко. Существенно большее значение непрерывное наращение имеет в количественном финансово-экономическом анализе сложных производственных и хозяйственных объектов и явлений, например, при выборе и обосновании инвестиционных решений. Необходимость в применении непрерывных наращений (или непрерывных процентов) определяется прежде всего тем, что многие экономические явления по своей природе непрерывны, поэтому аналитическое описание в виде непрерывных процессов более адекватно, чем на основе дискретных. Обобщим формулу сложных процентов для случая, когда проценты начисляются m раз в году:

S =P (1 + i/m) mn .

Наращенная сумма при дискретных процессах находится по этой формуле, здесь m - число периодов начисления в году, i - годовая или номинальная ставка. Чем больше m, тем меньше промежутки времени между моментами начисления процентов. В пределе при m ®¥ имеем:

`S = P (1 + i/m) mn = P ((1 + i/m) m) n .

Поскольку (1 + i/m) m = e i , то `S = P e in .

При непрерывном наращении процентов применяют особый вид процентной ставки - силу роста, которая характеризует относительный прирост наращенной суммы в бесконечно малом промежутке времени. При непрерывной капитализации процентов наращенная сумма равна конечной величине, зависящей от первоначальной суммы, срока наращения и номинальной ставки процентов. Для того, чтобы отличить ставки непрерывных процентов от ставки дискретных процентов, обозначим первую через d, тогда `S = Pe .

Сила роста d представляет собой номинальную ставку процентов при m®¥. Множитель наращения рассчитывается с помощью ЭВМ или по таблицам функции.

Потоки платежей. Финансовая рента

Контракты, сделки, коммерческие и производственно-хозяйственные операции часто предусматривают не отдельные разовые платежи, а множество распределенных во времени выплат и поступлений. Отдельные элементы такого ряда, а иногда и сам ряд платежей в целом, называется потоком платежей. Члены потока платежей могут быть как положительными (поступления), так и отрицательными (выплаты) величинами. Поток платежей, все члены которого положительные величины, а временные интервалы между двумя последовательными платежами постоянны, называют финансовой рентой. Ренты делятся на годовые и р-срочные, где р характеризует число выплат на протяжении года. Это дискретные ренты. В финансово-экономической практике встречаются и с последовательностями платежей, которые производятся так часто, что практически их можно рассматривать как непрерывные. Такие платежи описываются непрерывными рентами.

Пример 3.13. Пусть в конце каждого года в течение четырех лет в банк вносится по 1 млн. рублей, проценты начисляются в конце года, ставка - 5% годовых. В этом случае первый взнос обратится к концу срока ренты в величину 10 6 ´ 1,05 3 так как соответствующая сумма была на счете в течение 3 лет, второй взнос увеличится до 10 6 ´ 1,05 2 , так как был на счете 2 года. Последний взнос процентов не приносит. Таким образом, в конце срока ренты взносы с начисленными на них процентами представляют ряд чисел: 10 6 ´ 1,05 3 ; 10 6 ´ 1,05 2 ; 10 6 ´ 1,05; 10 6. Наращенная к концу срока ренты величина будет равна сумме членов этого ряда. Обобщим сказанное, выведем соответствующую формулу для наращенной суммы годовой ренты. Обозначим: S - наращенная сумма ренты, R - размер члена ренты, i - ставка процентов (десятичная дробь), n - срок ренты (число лет). Члены ренты будут приносить проценты в течение n - 1, n - 2,..., 2, 1 и 0 лет, а наращенная величина членов ренты составит

R (1 + i) n - 1 , R (1 + i) n - 2 ,..., R (1 + i), R.

Перепишем этот ряд в обратном порядке. Он представляет собой геометрическую прогрессию со знаменателем (1+i) и первым членом R. Найдем сумму членов прогрессии. Получим: S = R´((1 + i) n - 1)/((1 + i) - 1) = = R´((1 + i) n - 1)/ i. Обозначим S n; i =((1 + i) n - 1)/ i и будем называть его коэффициентом наращения ренты. Если же проценты начисляются m раз в году, то S = R´((1 + i/m) mn - 1)/((1 + i/m) m - 1), где i - номинальная ставка процентов.

Величина a n; i =(1 - (1 + i) - n)/ i называется коэффициентом приведения ренты. Коэффициент приведения ренты при n ®¥ показывает, во сколько раз современная величина ренты больше ее члена:

A n; i = (1 - (1 + i) - n)/ i =1/i.

Пример 3.14. Под вечной рентой понимается последовательность платежей, число членов которой не ограничено - она выплачивается в течение бесконечного числа лет. Вечная рента не является чистой абстракцией - на практике это некоторые виды облигационных займов, оценка способности пенсионных фондов отвечать по своим обязательствам. Исходя из сущности вечной ренты можно полагать, что ее наращенная сумма равна бесконечно большой величине, что легко доказать по формуле: R´((1 + i) n - 1)/ i ® ¥ при n ® ¥.

Коэффициент приведения для вечной ренты a n; i ® 1/i, откуда A = R/i, т. е. современная величина зависит только от величины члена ренты и принятой ставки процентов.

Метод потенциалов. Однако на распределительном методе основаны некоторые другие способы решения задач, что и вызывает необходимость его изучения. 9. Метод потенциалов Решение транспортной задачи любым способом производится на макете. Макет для применения метода потенциалов имеет следующий вид. Основная часть макета выделена двойными линиями. Она содержит k×l клеток. Каждая...

Признакам следует выделить два основных вида игр, несущих наибольшую образовательную нагрузку, так как все остальные являются производными от них. Этими видами являются инновационные игры и ансамблевые игры. Имитационные или ролевые игры позволяют обучать персонал практически с нуля, в то время как два предыдущих вида больше связаны с развивающим обучением. Назначение деловых игр Деловая...

Из остальных факторов мало что удастся сделать. Когда я поступил в корпорацию "Крайслер", то взял с собой мои записные книжки из компании "Форд", в которых была отражена служебная карьера нескольких сот фордовских менеджеров. После увольнения я набросал подробный перечень того, что не хотел оставлять в кабинете. Эти записные книжки в черных переплетах, несомненно, принадлежали мне, но можно было...

Научн. картине мира, кот. дает естествознание. Необходимость применения естствено научных методов и законов в практической деят-ти гуманитарных специальностей и привело к постановке того курса, кот. мы будем изучать: Физика для гуманитариев. (38) Связь между разделами естествознания. Слово естествознание представляет из себя сочетание 2х слов: естество (природа) и знание. В настоящее время...

Работа добавлена на сайт сайт: 2015-07-10

Заказать написание уникльной работы

;font-family:"Times New Roman"">ОГЛАВЛЕНИЕ

;font-family:"Times New Roman"">Введение………………………………………………………………………1

">Проценты……………………………………………………………………...2
">Применение простых и сложных процентов ;color:#000000">……………………………………………………………………6
;color:#000000">Применение простых процентов…………………………………………...7
;color:#000000">Применение сложных процентов…………………………………….…….9
">Сравнение методов простых и сложных процентов ;color:#000000">…………………………………………………………………..14
">Комбинированные схемы начисления процентов ;color:#000000">………………………………………………………………..…16
">Номинальная процентная ставка……………………………………………...........................................18
;color:#000000">Понятие номинальной процентной ставки…………………………….…19
;color:#000000">Эффективная процентная ставка……………………………………….…20
;color:#000000">Непрерывное начисление сложных процентов……………………..……21
">ПРОЦЕНТНЫЕ НАЧИСЛЕНИЯ……………………………………………...22

">Библиографический список………………………………………....25

">ЗАКЛЮЧЕНИЕ……..…………………………………………………….........26

">ПРАКТИЧЕСКАЯ ЧАСТЬ………………………………………………….....27

ВВЕДЕНИЕ

;font-family:"Times New Roman"">В любой развитой рыночной экономике процентная ставка в национальной валюте является одним из самых важных макроэкономических показателей, за которым пристально следят не только профессиональные финансисты, инвесторы и аналитики, но также предприниматели и простые граждане. Причина такого внимания ясна: процентная ставка - это самая главная цена в национальной экономике: она отражает цену денег во времени. Кроме того, двоюродная сестра процентной ставки - это уровень инфляции, измеряемый также в процентных пунктах и признаваемый в соответствии с монетаристской парадигмой одним из главных ориентиров и результатов состояния национальной экономики (чем меньше инфляция, тем лучше для экономики, и наоборот). Родственная связь здесь проста: уровень номинальной процентной ставки должен быть выше уровня инфляции, при этом оба показателя измеряются в процентах годовых. В современной экономической теории общий термин "процентная ставка" используется в единственном числе. Здесь она рассматривается в качестве инструмента, с помощью которого государство в лице монетарных властей воздействует на экономический цикл страны, сигнализируя об изменении кредитно-денежной политики и изменяя объем денежной массы в обращении.

;font-family:"Times New Roman"">Многообразие конкретных процентных ставок в национальной валюте - тема, которая является весьма полезным практическим знанием, накопление которого в жизни любого человека происходит эмпирическим путем. Благодаря средствам массовой информации, либо в своей профессиональной деятельности, либо при управлении личными сбережениями и инвестициями, мы все слышали или регулярно сталкиваемся с различными процентными ставками по разнообразным продуктам.

;font-family:"Times New Roman"">1. ПРОЦЕНТЫ

;font-family:"Times New Roman"">Процентами называют сумму, которую уплачивают за пользование денежными средствами. Это абсолютная величина дохода.

;font-family:"Times New Roman"">Отношение процентных денег, полученных за единицу времени, к величине капитала называется процентной ставкой, или таксой. Относительно момента выплаты или начисления дохода за пользование предоставленными денежными средствами проценты подразделяются на обычные и авансовые.

;font-family:"Times New Roman"">Обычные (декурсивные, ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">postnumerando ;font-family:"Times New Roman"">) проценты начисляются в конце периода относительно исходной величины средств. Доход на процент выплачивается в конце периодов финансовой операции.

;font-family:"Times New Roman"">Под периодом начисления процентов следует понимать отрезок времени между двумя следующими друг за другом процедурами взимания процентов или срок финансовой операции, если проценты начисляются один раз (рис. 1). Как видно из названия, эти проценты (обычные) применяются чаще, в большинстве депозитных и кредитных операций, а также в страховании.

;font-family:"Times New Roman"">Схема начисления процентов

;font-family:"Times New Roman"">Если же доход, определяемый процентом, выплачивается в момент предоставления кредита, то данная форма расчетов называется авансовой, или учетом, а применяемые проценты авансовыми (антисипативными, ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">prenumerando ;font-family:"Times New Roman"">), которые начисляется в начале периода относительно конечной суммы денег.

;font-family:"Times New Roman"">Доход на процент выплачивается в начале периода, в момент предоставления долга. Так рассчитывают проценты некоторых видах кредитования, например при продаже товаров в кредит, в международных расчетах, операциях с дисконтными ценными бумагами. При этом базой для расчета процентов служит сумма денег с процентами (сумма погашения долга), а исчисленные таким образом проценты взимаются вперед и являются авансом.

;font-family:"Times New Roman"">Существуют следующие виды процентных ставок:

;font-family:"Times New Roman"">Декурсивная ставка, ;font-family:"Times New Roman"">норма доходности ;font-family:"Times New Roman""> которой рассчитывается по начальной сумме кредита. Доход на процент выплачивается вместе с суммой кредита.

;font-family:"Times New Roman"">Антисипативная ставка, норма доходности которой рассчитывается по конечной сумме долга. Доход на процент выплачивается в момент предоставления кредита.

;font-family:"Times New Roman"">Действительная ставка, норма доходности которой соответствует получению дохода на процент один раз в год.

;font-family:"Times New Roman"">Номинальная ставка, доход на процент которой увеличивается кратное число раз в год.

;font-family:"Times New Roman"">Практика уплаты процентов основывается на теории наращивания денежных средств по арифметической или геометрической прогрессии.

;font-family:"Times New Roman"">Арифметическая прогрессия соответствует простым процентам, геометрическая сложным, т.е. в зависимости от того, что является базой для начисления переменная или постоянная величина.

;font-family:"Times New Roman"">Проценты делятся на:

;font-family:"Times New Roman"">- простые, которые весь срок обязательства начисляются на первоначальную сумму;

;font-family:"Times New Roman"">- сложные, база для начисления которых постоянно меняется за счет присоединения ранее начисленных процентов.

;font-family:"Times New Roman";color:#000000">Наращение может осуществляться по схеме простых и сложных процентов.

;font-family:"Times New Roman"">Формула наращения простых процентов (simpleinterest). Наращение простых процентов означает, что инвестируемая сумма ежегодно возрастает на величину PV r. В этом случае размер инвестированного капитала через n лет можно определить по формуле:

;font-family:"Times New Roman"">FV = PV (1 + r n).

;font-family:"Times New Roman"">Формула наращения сложных процентов (compoundinterest). Наращение по схеме сложных процентов означает, что очередной годовой доход исчисляется не с исходной величины инвестированного капитала, а с общей суммы, включающей также ранее начисленные и не востребованные инвестором проценты. В этом случае размер инвестированного капитала через n лет можно определить по формуле:

;font-family:"Times New Roman"">FV = PV (1 + r) ;font-family:"Times New Roman";vertical-align:super">n ;font-family:"Times New Roman"">.

;font-family:"Times New Roman"">При одном и том же значении процентной ставки:

;font-family:"Times New Roman"">1) темпы наращения сложных процентов выше темпов наращения простых, если период наращения превышает стандартный интервал начисления дохода;

;font-family:"Times New Roman"">2) темпы наращения сложных процентов меньше темпов наращения простых, если период наращения меньше стандартного интервала начисления дохода.

;font-family:"Times New Roman"">Области применения простых и сложных процентов. Простые и сложные проценты могут применяться как в отдельных операциях, так и одновременно. Области применения простых и сложных процентов можно разделить на три группы:

;font-family:"Times New Roman";color:#000000">1. операции с применением простых процентов;

;font-family:"Times New Roman";color:#000000">2. операции с применением сложных процентов;

;font-family:"Times New Roman";color:#000000">3. операции с одновременным применением простых и сложных процентов.

;font-family:"Times New Roman"">2 ПРИМЕНЕНИЕ ПРОСТЫХ И СЛОЖНЫХ ПРОЦЕНТОВ

">С экономической точки зрения метод сложных процентов является более обоснованным, так как он выражает возможность непрерывного реинвестирования (повторного вложения) денежных средств. Тем не менее, для краткосрочных (продолжительностью менее года) финансовых операций чаще всего используется метод простых процентов. Тому есть несколько причин:

;font-family:"Times New Roman"">Во-первых, и ещё несколько десятилетий назад это было достаточно актуально, расчёты с применением метода простых процентов намного проще, чем расчёты с применением метода сложных процентов.
;font-family:"Times New Roman"">Во-вторых, при небольших процентных ставках (в пределах 30%) и небольших промежутках времени (в пределах одного года) результаты, полученные с помощью метода простых процентов, довольно близки к результатам, полученным с применением метода сложных процентов (расхождение в пределах 1%). Если словосочетание «формула Тэйлора» вам о чём-то говорит, то вы поймёте, почему это так.
;font-family:"Times New Roman"">В-третьих, и, возможно, это основная причина, задолженность, найденная с помощью метода простых процентов для промежутка времени меньше года, всегда ;font-family:"Times New Roman"">больше ;font-family:"Times New Roman"">, чем задолженность, найденная с применением метода сложных процентов. Так как правила игры всегда диктует кредитор, то понятно, что в таком случае он выберет первый метод.

;font-family:"Times New Roman"">2.1 Применение простых процентов

Областью применения простых процентов чаще всего являются краткосрочные операции(со сроком до одного года) с однократным начислением процентов (краткосрочные ссуды, вексельные кредиты) и реже долгосрочные операции.

;font-family:"Times New Roman"">При краткосрочных операциях используется так называемая промежуточная процентная ставка, под которой понимается годовая процентная ставка, приведенная к сроку вложения денежных средств. Математически промежуточная процентная ставка равна доле годовой процентной ставки. Формула наращения простых процентов с использованием промежуточной процентной ставки имеет следующий вид:

;font-family:"Times New Roman";color:#000000">FV = PV (1 + f r),

;font-family:"Times New Roman";color:#000000">или

;font-family:"Times New Roman";color:#000000">FV = PV (1 + t r / Т),

;font-family:"Times New Roman";color:#000000">где f=t/T;

;font-family:"Times New Roman";color:#000000">t срок вложения денежных средств (при этом день вложения и день изъятия денежных средств принимаются за один день); Т расчетное количество дней в году.

;font-family:"Times New Roman"">Придолгосрочныхоперациях начисление простых процентов рассчитывается по формуле:

;font-family:"Times New Roman";color:#000000">FV = PV (1 + r n),

;font-family:"Times New Roman";color:#000000">где n срок вложения денежных средств (в годах). ,

;font-family:"Times New Roman"">2.2 Применение сложных процентов

;font-family:"Times New Roman";color:#000000">Областью применения сложных процентов являются долгосрочные операции (со сроком, превышающим год), в том числе предполагающие внутригодовое начисление процентов.

;font-family:"Times New Roman";color:#000000">В первом случае применяется обычная формула начисления сложных процентов:

;font-family:"Times New Roman";color:#000000">FV = PV (1 + r) ;font-family:"Times New Roman";vertical-align:super;color:#000000">n ;font-family:"Times New Roman";color:#000000">.

;font-family:"Times New Roman";color:#000000">Во втором случае применяется формула начисления сложных процентов с учетом внутригодового начисления. Под внутригодовым начислением процентов понимается выплата процентного дохода более одного раза в год. В зависимости от количества выплат дохода в год (m) внутригодовое начисление может быть:

;font-family:"Times New Roman";color:#000000">1) полугодовым (m = 2);

;font-family:"Times New Roman";color:#000000">2) поквартальным (m = 4);

;font-family:"Times New Roman";color:#000000">3) ежемесячным (m = 12);

;font-family:"Times New Roman";color:#000000">4) ежедневным (m = 365 или 366);

;font-family:"Times New Roman";color:#000000">5) непрерывным (m -» ?).

;font-family:"Times New Roman"">Формула наращения при полугодовом, поквартальном, ежемесячном и ежедневном начислении сложных процентов имеет следующий вид:

;font-family:"Times New Roman";color:#000000">FV = PV (1 + r / m) ;font-family:"Times New Roman";vertical-align:super;color:#000000">nm ;font-family:"Times New Roman";color:#000000">,

;font-family:"Times New Roman";color:#000000">где PV исходная сумма;

;font-family:"Times New Roman";color:#000000">г годовая процентная ставка;

;font-family:"Times New Roman";color:#000000">n количество лет;

;font-family:"Times New Roman";color:#000000">m количество внутригодовых начислений;

;font-family:"Times New Roman";color:#000000">FV наращенная сумма.

;font-family:"Times New Roman";color:#000000">Процентный доход при непрерывном начислении процентов рассчитывается по следующей формуле:

;font-family:"Times New Roman";color:#000000">FV ;font-family:"Times New Roman";vertical-align:sub;color:#000000">n ;font-family:"Times New Roman";color:#000000"> = Р e ;font-family:"Times New Roman";vertical-align:super;color:#000000">rn ;font-family:"Times New Roman";color:#000000">,

;font-family:"Times New Roman";color:#000000">или:

;font-family:"Times New Roman";color:#000000">FV ;font-family:"Times New Roman";vertical-align:sub;color:#000000">n ;font-family:"Times New Roman";color:#000000"> = P e ;font-family:"Times New Roman";vertical-align:super;color:#000000">?n ;font-family:"Times New Roman";color:#000000">,

;font-family:"Times New Roman";color:#000000">где: e = 2, 718281 трансцендентное число (число Эйлера);

;font-family:"Times New Roman";color:#000000">е ;font-family:"Times New Roman";vertical-align:super;color:#000000">?n ;font-family:"Times New Roman";color:#000000"> множитель наращения, который используется как при целом, так и дробном значении n;

;font-family:"Times New Roman";color:#000000">? специальное обозначение процентной ставки при непрерывном начислении процентов (непрерывная процентная ставка, «сила роста»);

;font-family:"Times New Roman";color:#000000">n количество лет.

;font-family:"Times New Roman"">При одинаковой величине исходной суммы, одинаковом сроке вложения денежных средств и значении процентной ставки возвращаемая сумма оказывается больше в случае использования формулы внутригодовых начислений, чем в случае использования обычной формулы начисления сложных процентов:

;font-family:"Times New Roman";color:#000000" xml:lang="en-US" lang="en-US">FV = PV (1 + r / m) ;font-family:"Times New Roman";vertical-align:super;color:#000000" xml:lang="en-US" lang="en-US">nm ;font-family:"Times New Roman";color:#000000" xml:lang="en-US" lang="en-US">> FV = PV (1 + r) ;font-family:"Times New Roman";vertical-align:super;color:#000000" xml:lang="en-US" lang="en-US">n ;font-family:"Times New Roman";color:#000000" xml:lang="en-US" lang="en-US">.

;font-family:"Times New Roman"">Если доход, полученный при использовании внутригодовых начислений, выразить в процентах, то полученная процентная ставка окажется выше той, которая использовалась при обычном начислении сложных процентов.

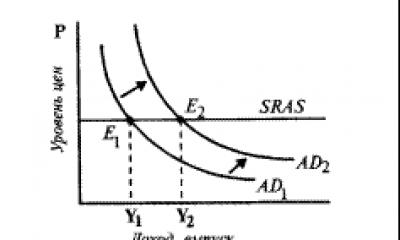
;font-family:"Times New Roman"">Таким образом, первоначально заявленная годовая процентная ставка для начисления сложных процентов, называемая номинальной, не отражает реальной эффективности сделки. Процентная ставка, отражающая фактически полученный доход, называется эффективной. Классификацию процентных ставок при внутригодовом начислении сложных процентов наглядно иллюстрирует рисунок.

;font-family:"Times New Roman"">Номинальная процентная ставка задается изначально. Для каждой номинальной процентной ставки и на ее основании можно рассчитать эффективную процентную ставку (r ;font-family:"Times New Roman";vertical-align:sub">е ;font-family:"Times New Roman"">).

;font-family:"Times New Roman"">Из формулы наращения сложных процентов можно получить формулу эффективной процентной ставки:

;font-family:"Times New Roman";color:#000000" xml:lang="en-US" lang="en-US">FV = PV (1 + r) ;font-family:"Times New Roman";vertical-align:super;color:#000000" xml:lang="en-US" lang="en-US">n ;font-family:"Times New Roman";color:#000000" xml:lang="en-US" lang="en-US">;

;font-family:"Times New Roman"">Приведем формулу наращения сложных процентов с внутригодовыми начислениями, при которых каждый год начисляется r / m процента:

;font-family:"Times New Roman";color:#000000">FV = PV (1 + r / m) ;font-family:"Times New Roman";vertical-align:super;color:#000000">nm ;font-family:"Times New Roman";color:#000000">.

;font-family:"Times New Roman";color:#000000">Тогда эффективная процентная ставка находится по формуле:

;font-family:"Times New Roman";color:#000000" xml:lang="en-US" lang="en-US">(1 + r ;font-family:"Times New Roman";vertical-align:sub;color:#000000" xml:lang="en-US" lang="en-US">e ;font-family:"Times New Roman";color:#000000" xml:lang="en-US" lang="en-US">) = (1 + r/m) ;font-family:"Times New Roman";vertical-align:super;color:#000000" xml:lang="en-US" lang="en-US">m ;font-family:"Times New Roman";color:#000000" xml:lang="en-US" lang="en-US">,

;font-family:"Times New Roman";color:#000000">или

;font-family:"Times New Roman";color:#000000" xml:lang="en-US" lang="en-US">r ;font-family:"Times New Roman";vertical-align:sub;color:#000000" xml:lang="en-US" lang="en-US">e ;font-family:"Times New Roman";color:#000000" xml:lang="en-US" lang="en-US"> = (l + r/m) ;font-family:"Times New Roman";vertical-align:super;color:#000000" xml:lang="en-US" lang="en-US">m ;font-family:"Times New Roman";color:#000000" xml:lang="en-US" lang="en-US">- 1,

;font-family:"Times New Roman";color:#000000">где r ;font-family:"Times New Roman";vertical-align:sub;color:#000000">е ;font-family:"Times New Roman";color:#000000"> эффективная процентная ставка; r номинальная процентная ставка; m количество внутригодовых выплат.

;font-family:"Times New Roman"">Величина эффективной процентной ставки зависит от количества внутригодовых начислений (m):

;font-family:"Times New Roman";color:#000000">1) при m = 1 номинальная и эффективная процентные ставки равны;

;font-family:"Times New Roman";color:#000000">2) чем больше количество внутригодовых начислений (значение m), тем больше эффективная процентная ставка.

;font-family:"Times New Roman"">Областью одновременного применения простых и сложных процентов являются долгосрочные операции, срок которых составляет дробное количество лет. При этом начисление процентов возможно двумя способами:

;font-family:"Times New Roman";color:#000000">1) начисление сложных процентов с дробным числом лет;

;font-family:"Times New Roman";color:#000000">2) начисление процентов по смешанной схеме.

;font-family:"Times New Roman"">В первом случае для расчетов применяется формула сложных процентов, в которой присутствует возведение в дробную степень:

;font-family:"Times New Roman";color:#000000">FV = PV (1 + r) ;font-family:"Times New Roman";vertical-align:super;color:#000000">n+f ;font-family:"Times New Roman";color:#000000">,

;font-family:"Times New Roman";color:#000000">где f дробная часть срока вложения денежных средств.

;font-family:"Times New Roman"">Во втором случае для расчетов применяется так называемая смешанная схема, которая включает формулу начисления сложных процентов с целым числом лет и формулу начисления простых процентов для краткосрочных операций:

;font-family:"Times New Roman";color:#000000">FV = PV (1 + r) ;font-family:"Times New Roman";vertical-align:super;color:#000000">n ;font-family:"Times New Roman";color:#000000"> (1 + f r),

;font-family:"Times New Roman";color:#000000">или

;font-family:"Times New Roman";color:#000000">FV = PV (1 + r) ;font-family:"Times New Roman";vertical-align:super;color:#000000">n ;font-family:"Times New Roman";color:#000000"> (1 + t r / Т) ;font-family:"Times New Roman";color:#52594f;display:none"> ;font-family:"Times New Roman";color:#52594f">.

;font-family:"Times New Roman";color:#000000">
;font-family:"Times New Roman"">3 СРАВНЕНИЕ МЕТОДОВ ПРОСТЫХ И СЛОЖНЫХ ПРОЦЕНТОВ

">Остановимся подробнее на второй и третьей причинах (так как первая очевидна). Если совместить приведённые в предыдущем параграфе графики роста задолженности, то получится следующая картина:

;color:#000000">
">Сравнение графиков роста задолженности по методам простых и сложных процентов.

">Таким образом, если используется одна и та же процентная ставка, то:

;font-family:"Times New Roman";color:#000000">для промежутков времени меньше года задолженность, найденная по методу простых процентов, всегда будет больше задолженности, найденной по методу сложных процентов;
;font-family:"Times New Roman";color:#000000">для промежутков времени больше года, наоборот, задолженность, найденная по методу сложных процентов, всегда будет больше задолженности, найденной по методу простых процентов;
;font-family:"Times New Roman";color:#000000">ну и, разумеется, для промежутка времени, равного одному году, результаты совпадают.

">При этом, если процентная ставка невелика, а промежуток времени меньше года, то S ;vertical-align:sub">сл ">(t) и S ;vertical-align:sub">пр ">(t) достаточно близки друг к другу. Однако всегда надо помнить, что если эти условия не выполняются, то расхождения в результатах могут быть значительными!

">Пример
В начале 90-х годов, в период сильной инфляции, российские банки предлагали очень большие исчисляемые сотнями процентов процентные ставки по рублёвым вкладам и кредитам.

">В качестве примера посмотрим, к каким расхождениям может привести использование простых процентов для полугодового вклада, когда процентная ставка составляет 300% годовых. Если размер вклада составляет S рублей, то через полгода на счету вкладчика будет сумма

" xml:lang="en-US" lang="en-US">\

">Если бы банк использовал сложные проценты, то итоговая сумма составила бы

" xml:lang="en-US" lang="en-US">\

">Разница в результатах составляет ½S , или 25% относительно сложного итога.

;font-family:"Times New Roman"">4 КОМБИНИРОВАННЫЕ СХЕМЫ НАЧИСЛЕНИЯ ПРОЦЕНТОВ

">На практике для продолжительных, но не целых промежутков времени особо щепетильные кредиторы иногда применяют комбинированную схему начисления процентов. При этом для целого числа лет используется метод сложных процентов, а для нецелого «остатка» метод простых процентов. Например, если ссуда размером 1 млн рублей выдана на 3 года и 73 дня (73 дня это 0,2 невисокосного года) под 10% годовых, то итоговая задолженность может быть найдена следующим способом:

;color:#000000" xml:lang="en-US" lang="en-US">\(S(3,2) = (1+0,1)^3 \cdot (1+0,1 \cdot 0,2) \cdot 1\ 000\ 000 = 1\ 357\ 620\) ;color:#000000">рублей ;color:#000000" xml:lang="en-US" lang="en-US">.

">Комбинирование простых и сложных процентов может также естественным образом возникать при многократном повторении одной и той же краткосрочной операции. К примеру, банки предлагают своим клиентам краткосрочные депозиты (вклады) на сроки от месяца до года. В течение периода действия депозитного договора увеличение суммы на счету вкладчика происходит по простой схеме. По окончании срока вклада происходит капитализация (присоединение процентных денег к исходной сумме). Если клиент не забирает деньги, то договор по вкладу пролонгируется на новый срок и базой для начисления процентов становится уже увеличенная сумма. Таким образом, с точки зрения клиента банка сумма вклада, оставленного на несколько сроков, будет расти по схеме сложных процентов:

">где t продолжительность того самого «базового» вклада, а n число периодов.

">Пример
Некий банк предлагает своим клиентам срочные вклады сроком на полгода под простую процентную ставку 10% годовых. Если клиент этого банка положил на депозит 200 000 рублей, а затем дважды продлевал договор по вкладу, то через полтора года он снял со своего счёта

;color:#000000" xml:lang="en-US" lang="en-US">\(S(1,5) = (1+0,1 \cdot \frac{1}{2})^3 \cdot 200\ 000 = 231\ 525\) ;color:#000000">рублей ;color:#000000" xml:lang="en-US" lang="en-US">.

;font-family:"Times New Roman"">5 НОМИНАЛЬНАЯ ПРОЦЕНТНАЯ СТАВКА

">С этого параграфа мы начинаем рассмотрение метода сложных процентов, не столь часто применяемого в кредитовании, как метод простых процентов, но широко распространённого в других областях финансов. В частности, метод сложных процентов используется для начисления процентных денег по долгосрочным вкладам (продолжительностью более года).

">Напомню, что смысл этого метода выражается фразой «начисление процентов на проценты». Это значит, что задолженность заёмщика в предыдущий момент времени служит основой для начисления процентов в следующий момент. При этом размер задолженности увеличивается в геометрической прогрессии (или в соответствии с показательной функцией, если считать время непрерывным). Например, если вкладчик положил в банк 100 тысяч рублей под сложную процентную ставку i = 6%, то через, скажем, пять месяцев на его счету будет сумма

;color:#000000">S(5/12) = (1 + i) ;vertical-align:super;color:#000000">5/12 ;color:#000000">S ;vertical-align:sub;color:#000000">0 ;color:#000000"> = 1,06 ;vertical-align:super;color:#000000">5/12 ;color:#000000"> · 100 000 ≈ 102 458 рублей.

;font-family:"Times New Roman"">5.1 Понятие номинальной процентной ставки

">Понятно, что без специальной техники производить такие вычисления не очень удобно, а до недавнего времени это было возможно только с помощью специальных таблиц сза табуированными множителями наращения. Чтобы уйти от необходимости извлекать громоздкие корни при расчётах с использованием сложных процентов, для задания сложных процентных ставок на практике применяются так называемые номинальные процентные ставки. Их суть заключается в следующем.

">Если вы положили деньги в банк, то проценты по вкладу будут начисляться не непрерывно, а с некоторой периодичностью раз в год, квартал, месяц или даже день. Этот процесс начисления процентных денег и их присоединения к сумме вклада называется «капитализацией процентов». Так вот, допустим, что капитализация процентов происходит m раз в год. Тогда, если известна j номинальная процентная ставка по вкладу, то каждый раз при начислении процентов сумма на счету вкладчика будет увеличиваться в(1 + \dfrac{j}{m}\) раз.

">Понятно, что по сути речь здесь идёт о применении комбинированной схемы простых и сложных процентов.

">Пример
Вкладчик положил на счёт в банке сумму в 200 тысяч рублей. Если номинальная процентная ставка по вкладу равна 8%, а проценты капитализируются раз в квартал (банк, разумеется, использует сложные проценты), то через полгода (то есть после двух начислений процентов) сумма на счету вкладчика будет составлять

;color:#000000">200 000 · (1 + 0,08/4) ;vertical-align:super;color:#000000">2 ;color:#000000"> = 208 080 рублей.

;font-family:"Times New Roman"">5.2 Эффективная процентная ставка

">Если задана номинальная процентная ставка, и капитализация процентов осуществляется m раз в год, то за год сумма вклада увеличится в

" xml:lang="en-US" lang="en-US">\(\left(1+ \dfrac{j}{m} \right)^m\)

">раз.

">Так как, с другой стороны, всегда должно выполняться соотношение для сложной процентной ставки:

" xml:lang="en-US" lang="en-US">S(1) = (1+ i) S ;vertical-align:sub" xml:lang="en-US" lang="en-US">0

">то

" xml:lang="en-US" lang="en-US">\[\tag{15.1} i = \left(1+ \frac{j}{m} \right)^m - 1\]

">Найденная таким образом сложная процентная ставка называется «эффективной», так как она, в отличие от номинальной ставки, характеризует настоящую доходность (эффективность) ссудной операции.

">Пример
Если номинальная ставка по вкладу равна 18%, и проценты начисляются каждый месяц, то эффективная процентная ставка будет составлять

;color:#000000" xml:lang="en-US" lang="en-US">\(i = \left(1+ \dfrac{0,18}{12} \right)^{12} - 1 \approx 0,1956 = 19,56\%\) ;color:#000000">годовых ;color:#000000" xml:lang="en-US" lang="en-US">,

">то есть на полтора процента больше, чем заявлено.

">Вообще говоря, эффективная процентная ставка всегда больше, чем номинальная. В этом нетрудно убедиться, разложив правую часть соотношения (15.1) по формуле бинома Ньютона.

;font-family:"Times New Roman"">5.3 Непрерывное начисление сложных процентов

">Как известно, для стремящегося к бесконечности числа x существует предел

" xml:lang="en-US" lang="en-US">\[\lim_{x \to \infty} \left(1 + \frac{1}{x} \right)^x = e,\]

">где e = 2,718281828... основание натуральных логарифмов. Эта формула называется вторым замечательным пределом. Из неё следует, в частности, что справедливо соотношение

">\[\ " xml:lang="en-US" lang="en-US">lim ">_{ " xml:lang="en-US" lang="en-US">m "> \ " xml:lang="en-US" lang="en-US">to "> \ " xml:lang="en-US" lang="en-US">infty ">} \ " xml:lang="en-US" lang="en-US">left ">(1 + \ " xml:lang="en-US" lang="en-US">frac ">{ " xml:lang="en-US" lang="en-US">j ">}{ " xml:lang="en-US" lang="en-US">m ">} \ " xml:lang="en-US" lang="en-US">right ">)^ " xml:lang="en-US" lang="en-US">m "> = " xml:lang="en-US" lang="en-US">e ">^ " xml:lang="en-US" lang="en-US">j ">\]

">Значит, если капитализация процентов осуществляется достаточно часто, например, ежедневно, то эффективную процентную ставку можно приближённо найти следующим образом:

">\[\ " xml:lang="en-US" lang="en-US">tag ">{15.2} " xml:lang="en-US" lang="en-US">i "> \ " xml:lang="en-US" lang="en-US">approxe ">^ " xml:lang="en-US" lang="en-US">j "> - 1\]

">Пример
Снова будем предполагать, что номинальная процентная ставка по вкладу составляет 18%, но капитализация процентов осуществляется ежедневно (m = 365). Точное значение эффективной процентной ставки, найденное по формуле (15.1), будет равно

">Если же использовать приближённую формулу (15.2), то можно получить следующий результат:

;color:#000000">i ≈ e ;vertical-align:super;color:#000000">0,18 ;color:#000000"> 1 = 0,197217...

">Как видите, расхождение совсем невелико.

6 Процентные начисления

;font-family:"Times New Roman";color:#000000">Для начисления процентов по вкладам (депозитам), да и кредитам тоже, применяются следующие формулы процентов:

;font-family:"Times New Roman";color:#000000">формула простых процентов,
;font-family:"Times New Roman";color:#000000">формула сложных процентов.

;font-family:"Times New Roman";color:#000000">Порядок начисления процентов формулам осуществляется с использованием фиксированной или плавающей ставки.

;font-family:"Times New Roman";color:#000000">Фиксированная ставка, это когда установленная по вкладу банка процентная ставка, закреплена в депозитном договоре и остается неизменной весь срок вложения средств, т.е. фиксируется. Такая ставка может измениться только в момент автоматической пролонгации договора на новый срок или при досрочном расторжении договорных отношений и выплате процентов за фактический срок вложения по ставке «до востребования», что оговаривается условиями.

;font-family:"Times New Roman";color:#000000">Плавающая ставка, это когда первоначально установленная по договору процентная ставка может меняться в течение всего срока вложения. Условия и порядок изменения ставок оговариваются в депозитном договоре. Процентные ставки могут изменяться: в связи с изменениями ставки рефинансирования, с изменением курса валюты, с переходом суммы вклада в другую категорию, и другими факторами.

;font-family:"Times New Roman";color:#000000">Для начисления процентов с применением формул, необходимо знать параметры вложения средств на депозитный счет, а именно:

;font-family:"Times New Roman";color:#000000">сумму вклада (депозита),
;font-family:"Times New Roman";color:#000000">процентную ставку по выбранному вкладу (депозиту),
;font-family:"Times New Roman";color:#000000">цикличность начисления процентов (ежедневно, ежемесячно, ежеквартально и т.д.),
;font-family:"Times New Roman";color:#000000">срок размещения вклада (депозита),
;font-family:"Times New Roman";color:#000000">иногда требуется и вид используемой процентной ставки - фиксированной или плавающей.

;font-family:"Times New Roman";color:#000000">Формула простых процентов применяется, если начисляемые на вклад проценты причисляются к вкладу только в конце срока депозита или вообще не причисляются, а переводятся на отдельный счет, т.е. расчет простых процентов не предусматривает капитализации процентов. При выборе вида вклада, на порядок начисления процентов стоит обращать внимание. Когда сумма вклада и срок размещения значительные, а банком применяется формула простых процентов, это приводит к занижению суммы процентного дохода вкладчика.

;font-family:"Times New Roman";color:#000000">Формула простых процентов по вкладам выглядит так:

;font-family:"Times New Roman";color:#000000">S сумма денежных средств, причитающихся к возврату вкладчику по окончании срока депозита. Она состоит из первоначальной суммы размещенных денежных средств, плюс начисленные проценты.

;font-family:"Times New Roman";color:#000000">

;font-family:"Times New Roman";color:#000000" xml:lang="en-US" lang="en-US">t ;font-family:"Times New Roman";color:#000000"> - количество дней начисления процентов по привлеченному вкладу.

;font-family:"Times New Roman";color:#000000">

;font-family:"Times New Roman";color:#000000">P первоначальная сумма привлеченных в депозит денежных средств.

;font-family:"Times New Roman";color:#000000">

;font-family:"Times New Roman";color:#000000">Если начисляемые по вкладу проценты, причисляются к вкладу через равные промежутки времени (ежедневно, ежемесячно, ежеквартально), то в этих случаях сумма процентов рассчитывается по формуле сложных процентов. Сложные проценты предусматривают капитализацию процентов (начисление процентов на проценты). Для расчета сложных процентов можно применять две формулы сложных процентов по вкладам, которые выглядят так:

;font-family:"Times New Roman";color:#000000">I годовая процентная ставка.

;font-family:"Times New Roman";color:#000000">t количество дней начисления процентов по привлеченному вкладу.

;font-family:"Times New Roman";color:#000000">K количество дней в календарном году (365 или 366).

;font-family:"Times New Roman";color:#000000">P сумма привлеченных в депозит денежных средств.

;font-family:"Times New Roman";color:#000000">Sp сумма процентов (доходов).

;font-family:"Times New Roman";color:#000000">n число периодов начисления процентов.

;font-family:"Times New Roman";color:#000000">S сумма вклада (депозита) с процентами.

;font-family:"Times New Roman";color:#000000">Однако, при расчете процентов проще сначала вычислить общую сумму вклада с процентами, и только затем вычислять сумму процентов (доходов). ;font-family:"Times New Roman"">
БИБЛИОРГРАФИЧЕСКИЙ СПИСОК

;font-family:"Times New Roman"">Техника финансово-экономических расчетов: Учеб.пособие. М.: Финансы и математика, 2000. 80с.: ил.
;font-family:"Times New Roman"">Джон К. ХаллГлава 4. Процентные ставки // Опционы, фьючерсы и другие производные финансовые инструменты = Options, FuturesandOtherDerivatives. 6-е изд. М.: ;font-family:"Times New Roman"">«Вильямс» ;font-family:"Times New Roman"">, 2007. С. 133-165.
;font-family:"Times New Roman"">http://forexaw.com/Cont-Economy/
;font-family:"Times New Roman"">http://www.bibliotekar.ru/
;font-family:"Times New Roman"">http://ru.wikipedia.org/

;font-family:"Times New Roman"">
ЗАКЛЮЧЕНИЕ

;font-family:"Times New Roman"">В настоящее время в условиях стабилизации экономики ниша услуг банковского кредитования для российского рынка еще не заполнена, т.е. можно выделить кредитование как наиболее перспективное средство получения доходов банками.

;font-family:"Times New Roman"">В условиях стабилизации экономики наметилась тенденция увеличения объема заимствований в промышленности и банкам для привлечения потенциальных заемщиков. Необходимо определить величину процентной ставки кредитования, как наиболее важный фактор, влияющий на выбор заемщиком того или иного банка, а, следовательно, необходимо более детально рассматривать составляющие, формирующие величину процентной ставки, влияющие на стоимость кредитов.

;font-family:"Times New Roman"">Также в условиях стабилизации экономики становится возможным расширение такого перспективного направления, обладающего огромным потенциалом кредитование потребительского сектора. И здесь процентная ставка также решает определяющую роль в привлечении частных кредитозаемщиков.

;font-family:"Times New Roman"">
ПРАКТИЧЕСКАЯ ЧАСТЬ

;font-family:"Times New Roman"">Задача 1

;font-family:"Times New Roman"">Банк предлагает 17 % годовых за размещение денежных средств на открываемых им депозитных счетах. Используя формулу дисконтирования, рассчитайте размер первоначального вклада, чтобы через 4 года иметь на счете 180 тыс. руб.

;font-family:"Times New Roman"">Решение

;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">S = P * (1+i) ;font-family:"Times New Roman";vertical-align:super" xml:lang="en-US" lang="en-US">n

;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">180 000 = P * (1+0,17) ;font-family:"Times New Roman";vertical-align:super" xml:lang="en-US" lang="en-US">4

;font-family:"Times New Roman"">180 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">000 = ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">P ;font-family:"Times New Roman""> * 1,8738

;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">P ;font-family:"Times New Roman""> = 96 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">061руб.

;font-family:"Times New Roman"">Ответ: для того, чтобы иметь на вкладе через 4 года 180 тыс. руб. необходимо, чтобы размер первоначального вклада составлял 96 061 рубль.

;font-family:"Times New Roman"">Задача 2

;font-family:"Times New Roman"">Гражданин получил в банке ипотечную ссуду в размере 1,5 млн руб. сроком на 8 лет на следующих условиях: для первого года процентная ставка сложных процентов равна 14% годовых; на следующие два года устанавливается маржа в размере 0,5% и на последующие годы маржа равна 0,7%. Найти сумму, которую гражданин должен вернуть в банк по окончании срока ссуды.

;font-family:"Times New Roman"">Решение

;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">S = P×((1+i1)*n1 +(1+i2)*n2 + …+(1+ik)*nk)

;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">S ;font-family:"Times New Roman""> = 1 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">500 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">000 × ((1+0,14) + (1+0,145)*2 + (1+0,152)*5)) = 1 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">500 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">000 *9,19 = 13 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">785 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">000 рублей.

;font-family:"Times New Roman"">Ответ: гражданин по окончанию срока ссуды должен вернуть в банк 13, 785 млн. рублей.

;font-family:"Times New Roman"">Задача 3

;font-family:"Times New Roman"">Организация, имея свободные денежные средства в размере 2-х млн руб., намерена инвестировать их на срок 5 лет. Возможны два варианта вложений, определите более выгодный из них:

;font-family:"Times New Roman"">а) средства вносятся на депозитный счет в банке с начислением процентов каждые 6 месяцев по ставке 18% годовых;

;font-family:"Times New Roman"">б) средства передаются другой организации в качестве ссуды с начислением 24% ежегодно.

;font-family:"Times New Roman"">Решение

;font-family:"Times New Roman"">а) ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">S ;font-family:"Times New Roman""> = 2 000 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">000 * (1+0,18/2) ;font-family:"Times New Roman";vertical-align:super">10 ;font-family:"Times New Roman"">= 2 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">000 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">000 * 2,37= 4 740 000 руб.

;font-family:"Times New Roman"">б) ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">S ;font-family:"Times New Roman""> = 2 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">000 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">000 * (1+0,24) ;font-family:"Times New Roman";vertical-align:super">5 ;font-family:"Times New Roman"">= 2 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">000 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">000 * 2,93 = 5 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">860 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">000 руб.

;font-family:"Times New Roman"">Ответ: второй вариант более выгодный.

;font-family:"Times New Roman"">Задача 4

;font-family:"Times New Roman"">Определите необходимую сумму вклада в настоящем, чтобы через два года иметь накопления в размере 150 тыс. руб. Годовая ставка процента 11%, начисление процентов производится 1 раз в квартал по схеме сложного процента.

;font-family:"Times New Roman"">Решение

;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">S = P * (1+i/m) ;font-family:"Times New Roman";vertical-align:super" xml:lang="en-US" lang="en-US">m*n

;font-family:"Times New Roman"">150 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">000 = ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">P ;font-family:"Times New Roman"">* ;font-family:"Times New Roman";vertical-align:super"> ;font-family:"Times New Roman"">(1+0,11/4) ;font-family:"Times New Roman";vertical-align:super">4*2

;font-family:"Times New Roman"">150 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">000 = ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">P ;font-family:"Times New Roman"">* (1+0,0275) ;font-family:"Times New Roman";vertical-align:super">8 ;font-family:"Times New Roman"">

;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">P ;font-family:"Times New Roman""> = 120 ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US"> ;font-family:"Times New Roman"">968

;font-family:"Times New Roman"">Ответ: необходимая сумма вклада - 120 968 рублей.

;font-family:"Times New Roman"">Задача 5

;font-family:"Times New Roman"">Через полгода после заключения финансового соглашения о получении кредита должник обязан заплатить 317 тыс. руб. Какова первоначальная величина кредита, если он выдан под 18% годовых и начисляются простые проценты с приближенным числом дней?

;font-family:"Times New Roman"">Решение

;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">S =P × (1+n×i)

;font-family:"Times New Roman"">где ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">S ;font-family:"Times New Roman""> - наращенная сумма,

;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">P ;font-family:"Times New Roman""> - сумма долга,

;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">n ;font-family:"Times New Roman""> - срок (доля от года),

;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">i ;font-family:"Times New Roman""> - ставка процента.

;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">P ;font-family:"Times New Roman""> = ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">S ;font-family:"Times New Roman"">/ (1+ ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">n ;font-family:"Times New Roman"">× ;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">i ;font-family:"Times New Roman"">)

;font-family:"Times New Roman"" xml:lang="en-US" lang="en-US">n ;font-family:"Times New Roman""> = 180/360 = 0,5.

;font-family:"Times New Roman"">Р = 317 000 / (1 + 0,5×0,18) = 317 000 /1, 09 = 290 826 руб.

;font-family:"Times New Roman"">Ответ: первоначальная величина кредита составила 290 826 рублей.

S = P(1 + i) n . (6.16)

Здесь P - первоначальная сумма, i - ставка процентов (в виде десятичной дроби), S - сумма, образовавшаяся к концу срока ссуды в конце n -го года. Рост по сложным процентам представляет собой процесс, развивающийся по геометрической прогрессии. Присоединение начисленных процентов к сумме, которая служила базой для их определения, часто называют капитализацией процентов. В финансовой практике часто сталкиваются с задачей, обратной определению наращенной суммы: по заданной сумме S, которую следует уплатить через некоторое время n , необходимо определить сумму полученной ссуды P. В этом случае говорят, что сумма S дисконтируется , а проценты в виде разности S - P называются дисконтом. Величину P, найденную дисконтированием S, называют современной, или приведенной, величиной S. Имеем:

P = ; P = = 0.

Таким образом, при очень больших сроках платежа современная величина последнего будет крайне незначительна. В практических финансово-кредитных операциях непрерывные процессы наращения денежных сумм, т. е. наращения за бесконечно малые промежутки времени, применяются редко. Существенно большее значение непрерывное наращение имеет в количественном финансово-экономическом анализе сложных производственных и хозяйственных объектов и явлений, например, при выборе и обосновании инвестиционных решений. Необходимость в применении непрерывных наращений (или непрерывных процентов) определяется прежде всего тем, что многие экономические явления по своей природе непрерывны, поэтому аналитическое описание в виде непрерывных процессов более адекватно, чем на основе дискретных. Обобщим формулу сложных процентов для случая, когда проценты начисляются m раз в году:

S =P (1 + i/m) mn .

Наращенная сумма при дискретных процессах находится по этой формуле, здесь m - число периодов начисления в году, i - годовая или номинальная ставка. Чем больше m , тем меньше промежутки времени между моментами начисления процентов. В пределе при m → ∞ имеем:

S = P (1 + i/m) mn = P ((1 + i/m) m) n .

Поскольку (1 + i/m) m = e i , то ` S = P e in .

При непрерывном наращении процентов применяют особый вид процентной ставки - силу роста , которая характеризует относительный прирост наращенной суммы в бесконечно малом промежутке времени. При непрерывной капитализации процентов наращенная сумма равна конечной величине, зависящей от первоначальной суммы, срока наращения и номинальной ставки процентов. Для того, чтобы отличить ставки непрерывных процентов от ставки дискретных процентов, обозначим первую через d , тогда S = Pe .

Сила роста d представляет собой номинальную ставку процентов при m → ∞. Множитель наращения рассчитывается с помощью ЭВМ или по таблицам функции.

Потоки платежей. Финансовая рента

Контракты, сделки, коммерческие и производственно-хозяйственные операции часто предусматривают не отдельные разовые платежи, а множество распределенных во времени выплат и поступлений. Отдельные элементы такого ряда, а иногда и сам ряд платежей в целом, называется потоком платежей . Члены потока платежей могут быть как положительными (поступления), так и отрицательными (выплаты) величинами. Поток платежей, все члены которого положительные величины, а временные интервалы между двумя последовательными платежами постоянны, называют финансовой рентой . Ренты делятся на годовые и р -срочные, где р характеризует число выплат на протяжении года. Это дискретные ренты. В финансово-экономической практике встречаются и с последовательностями платежей, которые производятся так часто, что практически их можно рассматривать как непрерывные. Такие платежи описываются непрерывными рентами.

Пример 3.13. Пусть в конце каждого года в течение четырех лет в банк вносится по 1 млн. рублей, проценты начисляются в конце года, ставка - 5% годовых. В этом случае первый взнос обратится к концу срока ренты в величину 10 6 ´ 1,05 3 так как соответствующая сумма была на счете в течение 3 лет, второй взнос увеличится до 10 6 ´ 1,05 2 , так как был на счете 2 года. Последний взнос процентов не приносит. Таким образом, в конце срока ренты взносы с начисленными на них процентами представляют ряд чисел: 10 6 ´ 1,05 3 ; 10 6 ´ 1,05 2 ; 10 6 ´ 1,05; 10 6. Наращенная к концу срока ренты величина будет равна сумме членов этого ряда. Обобщим сказанное, выведем соответствующую формулу для наращенной суммы годовой ренты. Обозначим: S - наращенная сумма ренты, R - размер члена ренты,
i - ставка процентов (десятичная дробь), n - срок ренты (число лет). Члены ренты будут приносить проценты в течение n - 1, n - 2,..., 2, 1 и 0 лет, а наращенная величина членов ренты составит

R (1 + i) n - 1 , R (1 + i) n - 2 ,..., R (1 + i), R.

Перепишем этот ряд в обратном порядке. Он представляет собой геометрическую прогрессию со знаменателем (1+i) и первым членом R. Найдем сумму членов прогрессии. Получим: S = R ´ ((1 + i) n - 1)/((1 + i) - 1) = R ´ ((1 + i) n - 1)/ i. Обозначим S n; i = ((1 + i) n - 1)/ i и будем называть его коэффициентом наращения ренты . Если же проценты начисляются m раз в году, то S = R ´ ((1 + i/m) mn - 1)/((1 + i/m) m - 1), где i - номинальная ставка процентов.

Величина a n; i = (1 - (1 + i) - n)/ i называется коэффициентом приведения ренты . Коэффициент приведения ренты при n → ∞ показывает, во сколько раз современная величина ренты больше ее члена:

a n; i = (1 - (1 + i) - n)/ i =1/i.

Пример 3.14. Под вечной рентой понимается последовательность платежей, число членов которой не ограничено - она выплачивается в течение бесконечного числа лет. Вечная рента не является чистой абстракцией - на практике это некоторые виды облигационных займов, оценка способности пенсионных фондов отвечать по своим обязательствам. Исходя из сущности вечной ренты можно полагать, что ее наращенная сумма равна бесконечно большой величине, что легко доказать по формуле:
R ×´ ((1 + i) n - 1)/ i → ∞ при n →∞.

Коэффициент приведения для вечной ренты a n; i → 1/i, откуда A = R/i, т. е. современная величина зависит только от величины члена ренты и принятой ставки процентов.

Страховые